import pandas as pd
import numpy as np
import altair as alt
import math
from scipy.stats import norm
from sklearn.cluster import AgglomerativeClustering
from typing import Dict
import json
from sklearn.cluster import KMeans
from collections import defaultdict
from scipy.stats import mode4 Estimate Distribution Parameters
Given \(S\), and a biomarker’s measurements, how can we estimate \(\mathcal N(\theta_{\mu}, \theta_{\sigma})\) and \(\mathcal N(\phi_{\mu}, \phi_{\sigma})\)?
output_dir = 'data'
df = pd.read_csv(f"{output_dir}/150|200_3.csv")
biomarkers = df.biomarker.unique()
idx = 1
biomarker_df = df[df.biomarker==biomarkers[idx]]
biomarker_df.sample(10)| participant | biomarker | measurement | k_j | S_n | affected_or_not | diseased | |
|---|---|---|---|---|---|---|---|
| 307 | 107 | PCC-FCI | 2.875619 | 10 | 2 | affected | True |
| 360 | 160 | PCC-FCI | 14.765535 | 0 | 2 | not_affected | False |
| 365 | 165 | PCC-FCI | 8.913005 | 0 | 2 | not_affected | False |
| 354 | 154 | PCC-FCI | 11.380722 | 0 | 2 | not_affected | False |
| 200 | 0 | PCC-FCI | 6.567299 | 0 | 2 | not_affected | False |
| 285 | 85 | PCC-FCI | 11.371021 | 0 | 2 | not_affected | False |
| 375 | 175 | PCC-FCI | 3.771693 | 9 | 2 | affected | True |
| 203 | 3 | PCC-FCI | 14.266635 | 0 | 2 | not_affected | False |
| 295 | 95 | PCC-FCI | 4.949612 | 0 | 2 | not_affected | False |
| 299 | 99 | PCC-FCI | 17.490539 | 0 | 2 | not_affected | False |
biomarker_df.shape(200, 7)4.1 Hard K-Means
To use this algorithm, we only need to know (1) whether this participant is diseased; and (2) each biomarker measurement.
The first method we can use is hard K-Means. We clustering a certain biomarker’s measurements into two clusters. A clustering is successful if:
- There are two, and only two clusters.
- Each clustes has more than one element (This is to make sure that the standard deviation of this biomarker’s theta or phi is non-zero)
Ideally, we wanted all healthy participants to be grouped into a single cluster, which is why we initially tried using the constrained K-Means algorithm implemented by Babaki (2017). However, the algorithm did not work as intended.
We therefore designed a hard k-means algorithm to satisfy our needs:
- We try hard K-Means multiple times; If the two above mentioned requirements are not met, then
- We group the measurements into two random clusters; If the two above mentioned requirements are still not met, then raise an error and stop.
Code
def compute_theta_phi_for_biomarker(biomarker_df, max_attempt = 50, seed = None):
"""get theta and phi parameters for this biomarker
input:
- biomarker_df: a pd.dataframe of a specific biomarker
output:
- a tuple: theta_mean, theta_std, phi_mean, phi_std
"""
if seed is not None:
# Set the seed for numpy's random number generator
rng = np.random.default_rng(seed)
else:
rng = np.random
n_clusters = 2
measurements = np.array(biomarker_df['measurement']).reshape(-1, 1)
healthy_df = biomarker_df[biomarker_df['diseased'] == False]
# clustering = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward')
# predictions = clustering.fit_predict(measurements)
# # Verify that AgglomerativeClustering produced exactly 2 clusters with more than 1 member each
# cluster_counts = np.bincount(predictions) # array([3, 2])
# if len(cluster_counts) != n_clusters or any(c <= 1 for c in cluster_counts):
# print("AgglomerativeClustering did not yield the required clusters, switching to KMeans.")
# # If AgglomerativeClustering fails, attempt KMeans with a max_attempt limit
curr_attempt = 0
n_init_value = 10
clustering_setup = KMeans(n_clusters=n_clusters, n_init=n_init_value)
while curr_attempt < max_attempt:
clustering_result = clustering_setup.fit(measurements)
predictions = clustering_result.labels_
cluster_counts = np.bincount(predictions) # array([3, 2])
if len(cluster_counts) == n_clusters and all(c > 1 for c in cluster_counts):
break
curr_attempt += 1
else:
print(f"KMeans failed. Try randomizing the predictions")
predictions = rng.choice([0, 1], size=len(measurements))
cluster_counts = np.bincount(predictions)
if len(cluster_counts) != n_clusters or not all(c > 1 for c in cluster_counts):
raise ValueError(f"KMeans clustering failed to find valid clusters within max_attempt.")
healthy_predictions = predictions[healthy_df.index]
mode_result = mode(healthy_predictions, keepdims=False).mode
phi_cluster_idx = mode_result[0] if isinstance(mode_result, np.ndarray) else mode_result
theta_cluster_idx = 1 - phi_cluster_idx
# two empty clusters to strore measurements
clustered_measurements = [[] for _ in range(2)]
# Store measurements into their cluster
for i, prediction in enumerate(predictions):
clustered_measurements[prediction].append(measurements[i][0])
# Calculate means and standard deviations
theta_mean, theta_std = np.mean(
clustered_measurements[theta_cluster_idx]), np.std(
clustered_measurements[theta_cluster_idx])
phi_mean, phi_std = np.mean(
clustered_measurements[phi_cluster_idx]), np.std(
clustered_measurements[phi_cluster_idx])
# Check for invalid values
if any(np.isnan(v) or v == 0 for v in [theta_std, phi_std, theta_mean, phi_mean]):
raise ValueError("One of the calculated values is invalid (0 or NaN).")
return theta_mean, theta_std, phi_mean, phi_std
def get_theta_phi_estimates(
data: pd.DataFrame,
) -> Dict[str, Dict[str, float]]:
"""
Obtain theta and phi estimates (mean and standard deviation) for each biomarker.
Args:
data (pd.DataFrame): DataFrame containing participant data with columns 'participant',
'biomarker', 'measurement', and 'diseased'.
# biomarkers (List[str]): A list of biomarker names.
Returns:
Dict[str, Dict[str, float]]: A dictionary where each key is a biomarker name,
and each value is another dictionary containing the means and standard deviations
for theta and phi of that biomarker, with keys 'theta_mean', 'theta_std', 'phi_mean',
and 'phi_std'.
"""
# empty hashmap of dictionaries to store the estimates
estimates = {}
biomarkers = data.biomarker.unique()
for biomarker in biomarkers:
# Filter data for the current biomarker
# reset_index is necessary here because we will use healthy_df.index later
biomarker_df = data[data['biomarker']
== biomarker].reset_index(drop=True)
theta_mean, theta_std, phi_mean, phi_std = compute_theta_phi_for_biomarker(
biomarker_df)
estimates[biomarker] = {
'theta_mean': theta_mean,
'theta_std': theta_std,
'phi_mean': phi_mean,
'phi_std': phi_std
}
return estimateshard_kmeans_estimates = get_theta_phi_estimates(data = df)
hard_kmeans_estimates_df = pd.DataFrame.from_dict(
hard_kmeans_estimates, orient='index')
hard_kmeans_estimates_df.reset_index(names = 'biomarker', inplace=True)
hard_kmeans_estimates_df| biomarker | theta_mean | theta_std | phi_mean | phi_std | |
|---|---|---|---|---|---|
| 0 | HIP-FCI | -8.587833 | 5.365053 | 4.903437 | 2.008974 |
| 1 | PCC-FCI | 7.288870 | 2.797150 | 14.569768 | 2.274322 |
| 2 | AB | 173.199732 | 33.778905 | 277.009573 | 34.503492 |
| 3 | P-Tau | -49.329924 | 15.988080 | -15.568346 | 12.688703 |
| 4 | MMSE | 22.272803 | 1.624078 | 28.011392 | 0.805532 |
| 5 | ADAS | -20.582091 | 3.853234 | -6.002048 | 1.487443 |
| 6 | HIP-GMI | 0.576991 | 0.157259 | 0.192231 | 0.128850 |
| 7 | AVLT-Sum | 27.808002 | 8.561387 | 52.524815 | 7.989840 |
| 8 | FUS-GMI | 0.519974 | 0.047474 | 0.628440 | 0.038051 |
| 9 | FUS-FCI | -7.061708 | 1.928477 | -12.647345 | 2.927590 |
with open('files/real_theta_phi.json', 'r') as f:
truth = json.load(f)
truth_df = pd.DataFrame.from_dict(truth, orient='index')
truth_df.reset_index(names = 'biomarker', inplace=True)
truth_df| biomarker | theta_mean | theta_std | phi_mean | phi_std | |
|---|---|---|---|---|---|
| 0 | MMSE | 22.0 | 2.666667 | 28.0 | 0.666667 |
| 1 | ADAS | -20.0 | 4.000000 | -6.0 | 1.333333 |
| 2 | AB | 150.0 | 16.666667 | 250.0 | 50.000000 |
| 3 | P-Tau | -50.0 | 33.333333 | -25.0 | 16.666667 |
| 4 | HIP-FCI | -5.0 | 6.666667 | 5.0 | 1.666667 |
| 5 | HIP-GMI | 0.3 | 0.333333 | 0.4 | 0.233333 |
| 6 | AVLT-Sum | 20.0 | 6.666667 | 40.0 | 15.000000 |
| 7 | PCC-FCI | 5.0 | 3.333333 | 12.0 | 4.000000 |
| 8 | FUS-GMI | 0.5 | 0.066667 | 0.6 | 0.066667 |
| 9 | FUS-FCI | -20.0 | 6.000000 | -10.0 | 3.333333 |
Now let’s compare the results using plots:
Code
def obtain_theta_phi_params(biomarker, estimate_df, truth):
'''This is to obtain both true and estimated theta and phi params for each biomarker '''
biomarker_data_est = estimate_df[estimate_df.biomarker == biomarker].reset_index()
biomarker_data = truth[truth.biomarker == biomarker].reset_index()
# theta for affected
theta_mean_est = biomarker_data_est.theta_mean[0]
theta_std_est = biomarker_data_est.theta_std[0]
theta_mean = biomarker_data.theta_mean[0]
theta_std = biomarker_data.theta_std[0]
# phi for not affected
phi_mean_est = biomarker_data_est.phi_mean[0]
phi_std_est = biomarker_data_est.phi_std[0]
phi_mean = biomarker_data.phi_mean[0]
phi_std = biomarker_data.phi_std[0]
return theta_mean, theta_std, theta_mean_est, theta_std_est, phi_mean, phi_std, phi_mean_est, phi_std_est
def make_chart(biomarkers, estimate_df, truth, title):
alt.renderers.enable('png')
charts = []
for biomarker in biomarkers:
theta_mean, theta_std, theta_mean_est, theta_std_est, phi_mean, phi_std, phi_mean_est, phi_std_est = obtain_theta_phi_params(
biomarker, estimate_df, truth)
mean1, std1 = theta_mean, theta_std
mean2, std2 = theta_mean_est, theta_std_est
# Generating points on the x axis
x_thetas = np.linspace(min(mean1 - 3*std1, mean2 - 3*std2),
max(mean1 + 3*std1, mean2 + 3*std2), 1000)
# Creating DataFrames for each distribution
df1 = pd.DataFrame({'x': x_thetas, 'pdf': norm.pdf(x_thetas, mean1, std1), 'Distribution': 'Actual'})
df2 = pd.DataFrame({'x': x_thetas, 'pdf': norm.pdf(x_thetas, mean2, std2), 'Distribution': 'Estimated'})
# Combining the DataFrames
df3 = pd.concat([df1, df2])
# Altair plot
chart_theta = alt.Chart(df3).mark_line().encode(
x='x',
y='pdf',
color=alt.Color('Distribution:N', legend=alt.Legend(title="Theta"))
).properties(
title=f'{biomarker}, Theta',
width=100,
height=100
)
mean1, std1 = phi_mean, phi_std
mean2, std2 = phi_mean_est, phi_std_est
# Generating points on the x axis
x_phis = np.linspace(min(mean1 - 3*std1, mean2 - 3*std2),
max(mean1 + 3*std1, mean2 + 3*std2), 1000)
# Creating DataFrames for each distribution
df1 = pd.DataFrame({'x': x_phis, 'pdf': norm.pdf(x_phis, mean1, std1), 'Distribution': 'Actual'})
df2 = pd.DataFrame({'x': x_phis, 'pdf': norm.pdf(x_phis, mean2, std2), 'Distribution': 'Estimated'})
# Combining the DataFrames
df3 = pd.concat([df1, df2])
# Altair plot
chart_phi = alt.Chart(df3).mark_line().encode(
x='x',
y='pdf',
color=alt.Color('Distribution:N', legend=alt.Legend(title="Phi"))
).properties(
title=f'{biomarker}, Phi',
width=100,
height=100
)
# Concatenate theta and phi charts horizontally
hconcat_chart = alt.hconcat(chart_theta, chart_phi).resolve_scale(color="independent")
# Append the concatenated chart to the list of charts
charts.append(hconcat_chart)
# Concatenate all the charts vertically
final_chart = alt.vconcat(*charts).properties(title = title)
# Display the final chart
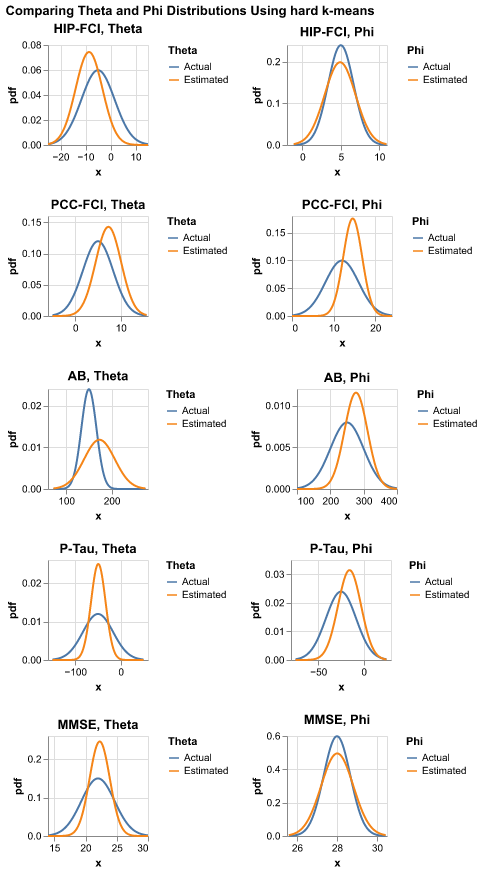
final_chart.display()make_chart(
biomarkers[0:5],
hard_kmeans_estimates_df,
truth_df,
title = "Comparing Theta and Phi Distributions Using hard k-means"
)It turns out the result is not very desriable.
4.2 Conjugate Priors
The second method we may utilize is conjugate priors. Conjugacy occurs when the posterior distribution is in the same family of distribution as the prior distribution, but with new parameter values.
Why conjugacy is important? Because without it, one has to do the integration, which oftentimes is hard.
Three major conjugate families:
- Beta-Binomial
- Gamma-Poisson
- Normal-Normal
In our example, we assume that the measurement data for each biomarker follows a normal distribution; however, we do not know the exact \(\mu\) and \(\sigma\). Our job is to estimate the two parameters for each biomarker based on the data we have.
According to An Introduction to Bayesian Thinking by Clyde et al. (2022), if the data comes from a normal distribution with unknown \(\mu\) and \(\sigma\), the conjugate prior for \(\mu\) has a normal distribution with mean \(m_0\) and variance \(\frac{\sigma^2}{n_0}\). The conjugate prior for \(\frac{1}{\sigma^2}\) has a Gamma distribution with shape \(\frac{v_0}{2}\) and rate \(\frac{v_0 s_0^{2}}{2}\) where
- \(m_0\): prior estimate of \(\mu\).
- \(n_0\): how strongly is the prior belief in \(m_0\) is held.
- \(s_0^2\): prior estimate of \(\sigma^2\).
- \(v_0\): prior degress of freedome, influencing the certainty of \(s_0^2\).
That is to say:
\[\mu | \sigma^2 \sim \mathcal{N}(m_0, \sigma^2/n_0)\]
\[1/\sigma^2 \sim Gamma\left(\frac{v_0}{2}, \frac{v_0 s_0^2}{2} \right)\]
Combined, we have:
\[(\mu, 1/\sigma^2) \sim NormalGamma(m_0, n_0, s_0^2, v_0)\]
The posterior also follows a Normal-Gamma distribution:
\[(\mu, 1/\sigma^2) | data \sim NormalGamma(m_n, n_n, s_n^2, v_n)\]
More specifically
\[1/\sigma^2 | data \sim Gamma(v_n/2, s_n^2 v_n/2)\]
\[\mu | data, \sigma^2 \sim \mathcal{N}(m_n, \sigma^2/n_n)\]
Based on the above two equations, we know that the mean of posterior mean is \(m_n\) and the mean of the posterior variance is \((s_n^2 v_n/2)/(v_n/2)\). This is beceause the expected value of \(Gamma(\alpha, \beta)\) is \(\frac{\alpha}{\beta}\).
where
- \(m_n\): posterior mean, mode, and median for \(\mu\)
- \(n_n\): posterior sample size
- \(s_n^2\): posterior variance
- \(v_n\): posterior degrees of freedome
The updating rules to get the new hyper-parameters:
\[m_n = \frac{n}{n+n_0} \bar{y} + \frac{n_0}{n+n_0}m_0\]
\[n_n = n_0 + n\]
\[v_n = v_0 + n\]
\[s_n^2 = \frac{1}{v_n}\left[s^2(n-1) + s_0^2v_0 + \frac{n_0n}{n_n}(\bar{y}-m_0)^2\right]\]
where
- \(n\): sample size
- \(\bar{y}\): sample mean
- \(s^2\): sample variance
To apply the algorithm of conjugate priors, we assume we already know \(S\) and \(k_j\), alongside biomarker measurement (\(X_{nj}\)). Based on \(S\) and \(k_j\), we can infer whether a biomarker is affected by the disease or not.
Code
def estimate_params_exact(m0, n0, s0_sq, v0, data):
'''This is to estimate means and vars based on conjugate priors
Inputs:
- data: a vector of measurements
- m0: prior estimate of $\mu$.
- n0: how strongly is the prior belief in $m_0$ is held.
- s0_sq: prior estimate of $\sigma^2$.
- v0: prior degress of freedome, influencing the certainty of $s_0^2$.
Outputs:
- mu estiate, std estimate
'''
# Data summary
sample_mean = np.mean(data)
sample_size = len(data)
sample_var = np.var(data, ddof=1) # ddof=1 for unbiased estimator
# Update hyperparameters for the Normal-Inverse Gamma posterior
updated_m0 = (n0 * m0 + sample_size * sample_mean) / (n0 + sample_size)
updated_n0 = n0 + sample_size
updated_v0 = v0 + sample_size
updated_s0_sq = (1 / updated_v0) * ((sample_size - 1) * sample_var + v0 * s0_sq +
(n0 * sample_size / updated_n0) * (sample_mean - m0)**2)
updated_alpha = updated_v0/2
updated_beta = updated_v0*updated_s0_sq/2
# Posterior estimates
mu_posterior_mean = updated_m0
sigma_squared_posterior_mean = updated_beta/updated_alpha
mu_estimation = mu_posterior_mean
std_estimation = np.sqrt(sigma_squared_posterior_mean)
return mu_estimation, std_estimation
def get_theta_phi_conjugate_priors(biomarkers, data_we_have, theta_phi_kmeans):
'''To get estimated parameters, returns a hashmap
Input:
- biomarkers: biomarkers
- data_we_have: participants data filled with initial or updated participant_stages
- theta_phi_kmeans: a hashmap of dicts, which are the prior theta and phi values
obtained from the initial hard k-means algorithm
Output:
- a hashmap of dictionaries. Key is biomarker name and value is a dictionary.
Each dictionary contains the theta and phi mean/std values for a specific biomarker.
'''
# empty list of dictionaries to store the estimates
hashmap_of_means_stds_estimate_dicts = {}
for biomarker in biomarkers:
# Initialize dictionary outside the inner loop
dic = {'biomarker': biomarker}
for affected in ['affected', 'not_affected']:
data_full = data_we_have[(data_we_have.biomarker == biomarker) & (
data_we_have.affected_or_not == affected)]
if len(data_full) > 1:
measurements = data_full.measurement
s0_sq = np.var(measurements, ddof=1)
m0 = np.mean(measurements)
mu_estimate, std_estimate = estimate_params_exact(
m0=m0, n0=1, s0_sq=s0_sq, v0=1, data=measurements)
if affected == 'affected':
dic['theta_mean'] = mu_estimate
dic['theta_std'] = std_estimate
else:
dic['phi_mean'] = mu_estimate
dic['phi_std'] = std_estimate
# If there is only one observation or not observation at all, resort to theta_phi_kmeans
# YES, IT IS POSSIBLE THAT DATA_FULL HERE IS NULL
# For example, if a biomarker indicates stage of (num_biomarkers), but all participants' stages
# are smaller than that stage; so that for all participants, this biomarker is not affected
else:
print('not enough data here, so we have to use theta phi estimates from hard k-means')
# print(theta_phi_kmeans)
if affected == 'affected':
dic['theta_mean'] = theta_phi_kmeans[biomarker]['theta_mean']
dic['theta_std'] = theta_phi_kmeans[biomarker]['theta_std']
else:
dic['phi_mean'] = theta_phi_kmeans[biomarker]['phi_mean']
dic['phi_std'] = theta_phi_kmeans[biomarker]['phi_std']
# print(f"biomarker {biomarker} done!")
hashmap_of_means_stds_estimate_dicts[biomarker] = dic
return hashmap_of_means_stds_estimate_dictsconjugate_prior_theta_phi = get_theta_phi_conjugate_priors(
biomarkers = biomarkers,
data_we_have = df,
theta_phi_kmeans = hard_kmeans_estimates
)
cp_df = pd.DataFrame.from_dict(conjugate_prior_theta_phi, orient='index')
cp_df.reset_index(drop=True, inplace=True)
cp_df| biomarker | theta_mean | theta_std | phi_mean | phi_std | |
|---|---|---|---|---|---|
| 0 | HIP-FCI | -5.378366 | 7.233991 | 5.092800 | 1.514402 |
| 1 | PCC-FCI | 5.521792 | 2.777207 | 12.071769 | 3.671679 |
| 2 | AB | 151.143708 | 14.806694 | 251.973564 | 51.382188 |
| 3 | P-Tau | -41.768257 | 34.857945 | -24.739527 | 14.928907 |
| 4 | MMSE | 23.122406 | 2.446874 | 28.049683 | 0.718493 |
| 5 | ADAS | -19.633304 | 4.582900 | -5.902198 | 1.278311 |
| 6 | HIP-GMI | 0.425625 | 0.272876 | 0.379542 | 0.235348 |
| 7 | AVLT-Sum | 21.664360 | 3.755735 | 40.700638 | 14.480463 |
| 8 | FUS-GMI | 0.482745 | 0.055585 | 0.590434 | 0.063730 |
| 9 | FUS-FCI | -18.566905 | 5.781937 | -9.648705 | 3.099195 |
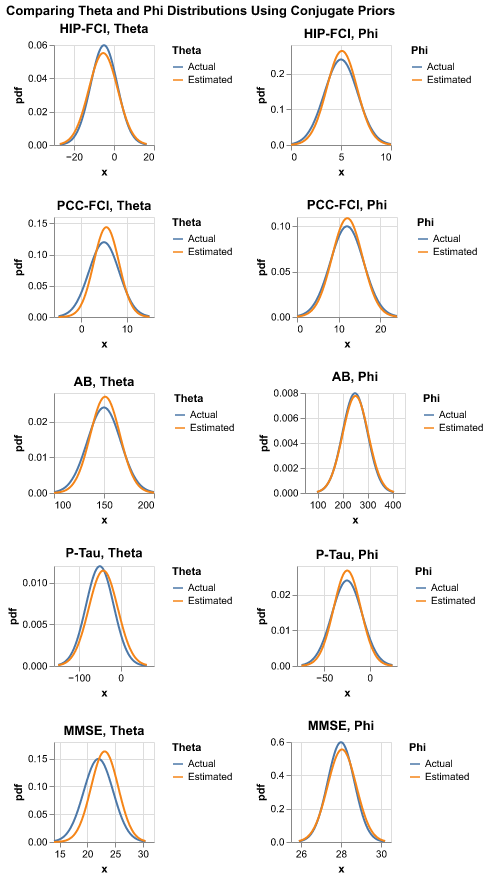
When we estimate \(\theta\) and \(\phi\) using conjugate priors, we need to use the result from hard k-means as a fall back because it is possible that for a specific biomarker, either the affected or the not_affected group is empty. If that is the case, we are not able to estimate relevant parameters and have to resort to the fallback result.
4.3 Soft K-Means
Conjugate Priors assumes we know \(k_j\), which often times is not already known. Our hard k-means algorithm is only taking advantage of \(X_{nj}\) and whether participants are diseased or not, leaving \(S\), which is known to us, unexploited.
Soft K-Means is a good alternative to these two because it utilizes \(S\) while at the same time do not assume we know \(k_j\).
The logic of soft-kmeans is this;
- If a participant is diseased, we iterate through all possible disease stages, and calculate the associated likelihood using Equation 2.1. We then normalize these likelihoods to obtain the estimated probability of this participant being at each stage. For example, if there are three possible stages, and the associated likelihoods are
[1, 3, 6], then the normalized likelihoods would be[0.1, 0.3, 0.6].
You may wonder how we can use Equation 2.1 when we do not know \(\theta\) and \(\phi\) yet (which is exactly what we are trying to do!). If you notice this, it is a very keen observation!.
If fact, we are going to use the estimated \(\theta\) and \(\phi\) we obtained above using hard k-means.
- For each biomarker \(n\), we obtain \(S_n\) based on \(S\). Then we iterate through all participants. If this participant is healthy, we include their biomarker measurement in
cluster_phi. If this participant is diseased, we compare between \(P_{\theta}\) and \(P_{\phi}\). If \(S_n = 2\), then \(P_{\theta} = 0.1 + 0.3 = 0.4\) and \(P_{\phi} = 0.6\). Because \(P_{\phi}\) is larger, we include this participant’s biomarker measurement incluster_phi. When the iteration through participants is done, we can calculate the mean and standard deviation of each cluster.
If \(P_{\theta} = P_{\phi}\), we randomly assign this participant’s biomarker measurement to a cluster.
Code
def compute_single_measurement_likelihood(theta_phi, biomarker, affected, measurement):
'''Computes the likelihood of the measurement value of a single biomarker
We know the normal distribution defined by either theta or phi
and we know the measurement. This will give us the probability
of this given measurement value.
input:
- theta_phi: the dictionary containing theta and phi values for each biomarker
- biomarker: an integer between 0 and 9
- affected: boolean
- measurement: the observed value for a biomarker in a specific participant
output: a scalar
'''
biomarker_dict = theta_phi[biomarker]
mu = biomarker_dict['theta_mean'] if affected else biomarker_dict['phi_mean']
std = biomarker_dict['theta_std'] if affected else biomarker_dict['phi_std']
var = std**2
if var <= int(0) or np.isnan(measurement) or np.isnan(mu):
print(f"Invalid values: measurement: {measurement}, mu: {mu}, var: {var}")
likelihood = np.exp(-(measurement - mu)**2 /
(2 * var)) / np.sqrt(2 * np.pi * var)
else:
likelihood = np.exp(-(measurement - mu)**2 /
(2 * var)) / np.sqrt(2 * np.pi * var)
return likelihood
def fill_up_kj_and_affected(pdata, k_j):
'''Fill up a single participant's data using k_j; basically add two columns:
k_j and affected
Note that this function assumes that pdata already has the S_n column
Input:
- pdata: a dataframe of ten biomarker values for a specific participant
- k_j: a scalar
'''
data = pdata.copy()
data['k_j'] = k_j
data['affected'] = data.apply(lambda row: row.k_j >= row.S_n, axis=1)
return data
def compute_likelihood(pdata, k_j, theta_phi):
'''
This function computes the likelihood of seeing this sequence of biomarker values
for a specific participant, assuming that this participant is at stage k_j
'''
data = fill_up_kj_and_affected(pdata, k_j)
likelihood = 1
for i, row in data.iterrows():
biomarker = row['biomarker']
measurement = row['measurement']
affected = row['affected']
likelihood *= compute_single_measurement_likelihood(
theta_phi, biomarker, affected, measurement)
return likelihood
def obtain_participants_hashmap(
data,
prior_theta_phi_estimates,
):
"""
Input:
- data: a pd.dataframe. For exrample, 150|200_3.csv
- prior_theta_phi_estimates, a hashmap of dicts.
This is the result from hard k-means
Output:
- hashmap: a dictionary whose key is participant id
and value value is a dict whose key is stage
and value is normalized likelihood
"""
# initialize hashmap_of_normalized_stage_likelihood_dicts
participants_hashmap = {}
non_diseased_participants = data[
data.diseased == False]['participant'].unique()
disease_stages = data.S_n.unique()
for p in data.participant.unique():
dic = defaultdict(int)
pdata = data[data.participant == p].reset_index(drop = True)
if p in non_diseased_participants:
dic[0] = 1
else:
for k_j in disease_stages:
kj_ll = compute_likelihood(pdata, k_j, prior_theta_phi_estimates)
dic[k_j] = kj_ll
# likelihood sum
sum_ll = sum(dic.values())
epsilon = 1e-10
if sum_ll == 0:
sum_ll = epsilon
normalized_lls = [l/sum_ll for l in dic.values()]
normalized_ll_dict = dict(zip(disease_stages, normalized_lls))
participants_hashmap[p] = normalized_ll_dict
return participants_hashmap
def calc_soft_kmeans_for_biomarker(
data,
biomarker,
participants_hashmap
):
"""obtain theta, phi estimates using soft kmeans for a single biomarker
Inputs:
- data: a pd.dataframe. For example, 150|200_3.csv
- biomarker: a str, a certain biomarker name
- hashmap: a dict, returned result of obtain_hashmap()
Outputs:
- theta_mean, theta_std, phi_mean, phi_std, a tuple of floats
"""
non_diseased_participants = data[
data.diseased == False]['participant'].unique()
disease_stages = data.S_n.unique()
# DataFrame for this biomarker
biomarker_df = data[
data['biomarker'] == biomarker].reset_index(
drop=True).sort_values(
by = 'participant', ascending = True)
# Extract measurements
measurements = np.array(biomarker_df['measurement'])
this_biomarker_order = biomarker_df.S_n[0]
affected_cluster = []
non_affected_cluster = []
for p in data.participant.unique():
if p in non_diseased_participants:
non_affected_cluster.append(measurements[p])
else:
normalized_ll_dict = participants_hashmap[p]
affected_prob = sum(
normalized_ll_dict[
kj] for kj in disease_stages if kj >= this_biomarker_order)
non_affected_prob = sum(
normalized_ll_dict[
kj] for kj in disease_stages if kj < this_biomarker_order)
if affected_prob > non_affected_prob:
affected_cluster.append(measurements[p])
elif affected_prob < non_affected_prob:
non_affected_cluster.append(measurements[p])
else:
# Assign to either cluster randomly if probabilities are equal
if np.random.random() > 0.5:
affected_cluster.append(measurements[p])
else:
non_affected_cluster.append(measurements[p])
# Compute means and standard deviations
theta_mean = np.mean(affected_cluster) if affected_cluster else np.nan
theta_std = np.std(affected_cluster) if affected_cluster else np.nan
phi_mean = np.mean(
non_affected_cluster) if non_affected_cluster else np.nan
phi_std = np.std(non_affected_cluster) if non_affected_cluster else np.nan
return theta_mean, theta_std, phi_mean, phi_std
def cal_soft_kmeans_for_biomarkers(
data,
participants_hashmap,
prior_theta_phi_estimates,
):
soft_kmeans_estimates = {}
biomarkers = data.biomarker.unique()
for biomarker in biomarkers:
dic = {'biomarker': biomarker}
prior = prior_theta_phi_estimates[biomarker]
theta_mean, theta_std, phi_mean, phi_std = calc_soft_kmeans_for_biomarker(
data, biomarker, participants_hashmap
)
if theta_std == 0 or math.isnan(theta_std):
theta_mean = prior['theta_mean']
theta_std = prior['theta_std']
if phi_std == 0 or math.isnan(phi_std):
phi_mean = prior['phi_mean']
phi_std = prior['phi_std']
dic['theta_mean'] = theta_mean
dic['theta_std'] = theta_std
dic['phi_mean'] = phi_mean
dic['phi_std'] = phi_std
soft_kmeans_estimates[biomarker] = dic
return soft_kmeans_estimatesparticipants_hashmap = obtain_participants_hashmap(
data = df,
prior_theta_phi_estimates = hard_kmeans_estimates,
)
soft_kmeans_estimates = cal_soft_kmeans_for_biomarkers(
data = df,
participants_hashmap = participants_hashmap,
prior_theta_phi_estimates = hard_kmeans_estimates,
)soft_kmeans_estimates_df = pd.DataFrame.from_dict(
soft_kmeans_estimates, orient='index')
soft_kmeans_estimates_df.reset_index(drop=True, inplace=True)
soft_kmeans_estimates_df| biomarker | theta_mean | theta_std | phi_mean | phi_std | |
|---|---|---|---|---|---|
| 0 | HIP-FCI | -5.378366 | 7.232544 | 5.092800 | 1.514369 |
| 1 | PCC-FCI | 5.710289 | 2.864833 | 12.098428 | 3.688180 |
| 2 | AB | 153.648672 | 18.041801 | 253.189546 | 51.038112 |
| 3 | P-Tau | -42.235505 | 34.734178 | -24.626343 | 14.860556 |
| 4 | MMSE | 23.122406 | 2.445751 | 28.049683 | 0.718480 |
| 5 | ADAS | -18.374956 | 5.810630 | -5.889272 | 1.283121 |
| 6 | HIP-GMI | 0.442551 | 0.261505 | 0.373983 | 0.234485 |
| 7 | AVLT-Sum | 23.819301 | 6.942910 | 41.371798 | 14.381565 |
| 8 | FUS-GMI | 0.496420 | 0.052929 | 0.595958 | 0.060867 |
| 9 | FUS-FCI | -6.326653 | 1.695438 | -10.205164 | 3.733813 |
4.4 Conclusion
We compare the above three methods. Hard k-means has the least number of prerequisites: it only needs to know whether participants are healthy or not and biomarker measurements. However, the drawback is that it might not be very accurate. Conjugate priors are extremely accurate; however, it requires knowledge of almost everything: besides what is required by hard k-means, it also requires \(S\) and \(k_j\). Soft k-kmeans does not require the knowledge of \(k_j\) and is an improvement over hard k-means.
We also noticed that both conjugate priors and soft k-means need to use the result from hard k-means as a fallback.