import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import json
import scipy.stats as stats
from typing import List, Optional, Tuple, Dict
import os
import seaborn as sns
import altair as alt 3 Generate Synthetic Data
In this chapter, we talk about how we generate the synthetic data of participants’ biomarker measurements. These data are used to test our algorithms.
3.1 Obtain Estimated Distribution Parameters
In Section 2.4, we mentioned that EBM can be used as a generative model and we need to know \(S, \theta, \phi\) and \(k_j\).
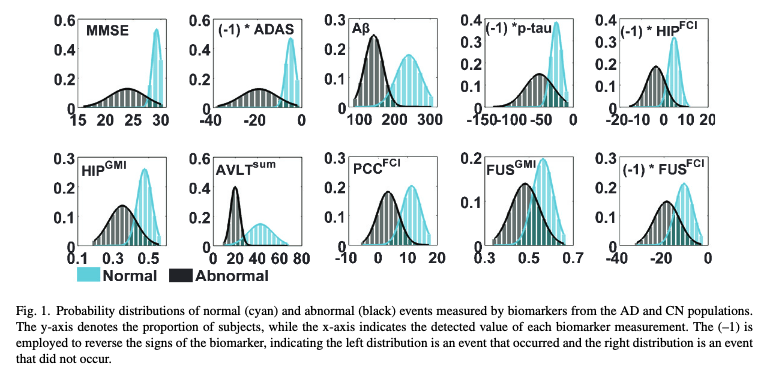
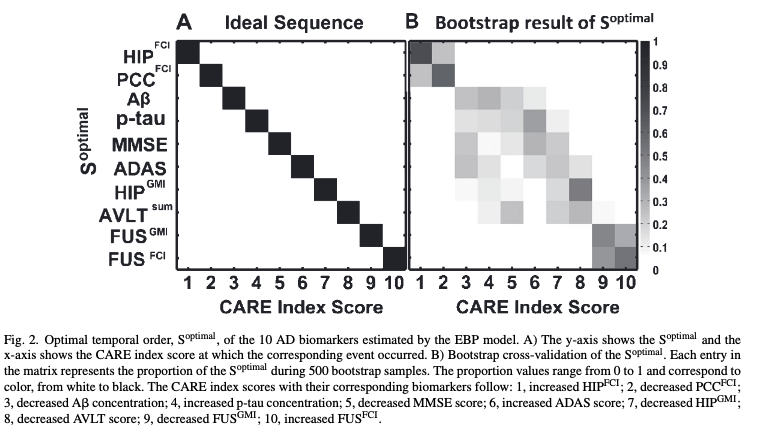
First, we obtained \(S, \theta, \phi\) from Chen et al. (2016):
This is our estimation:
Code
all_ten_biomarker_names = np.array([
'MMSE', 'ADAS', 'AB', 'P-Tau', 'HIP-FCI',
'HIP-GMI', 'AVLT-Sum', 'PCC-FCI', 'FUS-GMI', 'FUS-FCI'])
# in the order above
# cyan, normal
phi_means = [28, -6, 250, -25, 5, 0.4, 40, 12, 0.6, -10]
# black, abnormal
theta_means = [22, -20, 150, -50, -5, 0.3, 20, 5, 0.5, -20]
# cyan, normal
phi_std_times_three = [2, 4, 150, 50, 5, 0.7, 45, 12, 0.2, 10]
phi_stds = [std_dev/3 for std_dev in phi_std_times_three]
# black, abnormal
theta_std_times_three = [8, 12, 50, 100, 20, 1, 20, 10, 0.2, 18]
theta_stds = [std_dev/3 for std_dev in theta_std_times_three]
# to get the real_theta_phi means and stds
hashmap_of_dicts = {}
for i, biomarker in enumerate(all_ten_biomarker_names):
dic = {}
# dic = {"biomarker": biomarker}
dic['theta_mean'] = theta_means[i]
dic['theta_std'] = theta_stds[i]
dic['phi_mean'] = phi_means[i]
dic['phi_std'] = phi_stds[i]
hashmap_of_dicts[biomarker] = dic
hashmap_of_dicts
real_theta_phi = pd.DataFrame(hashmap_of_dicts).transpose().reset_index(names=['biomarker'])
real_theta_phi| biomarker | theta_mean | theta_std | phi_mean | phi_std | |
|---|---|---|---|---|---|
| 0 | MMSE | 22.0 | 2.666667 | 28.0 | 0.666667 |
| 1 | ADAS | -20.0 | 4.000000 | -6.0 | 1.333333 |
| 2 | AB | 150.0 | 16.666667 | 250.0 | 50.000000 |
| 3 | P-Tau | -50.0 | 33.333333 | -25.0 | 16.666667 |
| 4 | HIP-FCI | -5.0 | 6.666667 | 5.0 | 1.666667 |
| 5 | HIP-GMI | 0.3 | 0.333333 | 0.4 | 0.233333 |
| 6 | AVLT-Sum | 20.0 | 6.666667 | 40.0 | 15.000000 |
| 7 | PCC-FCI | 5.0 | 3.333333 | 12.0 | 4.000000 |
| 8 | FUS-GMI | 0.5 | 0.066667 | 0.6 | 0.066667 |
| 9 | FUS-FCI | -20.0 | 6.000000 | -10.0 | 3.333333 |
Store the parameters to a JSON file:
with open('files/real_theta_phi.json', 'w') as fp:
json.dump(hashmap_of_dicts, fp)Code
biomarkers = all_ten_biomarker_names
n_biomarkers = len(biomarkers)
def plot_distribution_pair(ax, mu1, sigma1, mu2, sigma2, title):
"""mu1, sigma1: theta
mu2, sigma2: phi
"""
xmin = min(mu1 - 4*sigma1, mu2-4*sigma2)
xmax = max(mu1 + 4*sigma1, mu2 + 4*sigma2)
x = np.linspace(xmin, xmax, 1000)
y1 = stats.norm.pdf(x, loc = mu1, scale = sigma1)
y2 = stats.norm.pdf(x, loc = mu2, scale = sigma2)
ax.plot(x, y1, label = "Abnormal", color = "black")
ax.plot(x, y2, label = "Normal", color = "cyan")
ax.fill_between(x, y1, alpha = 0.3, color = "black")
ax.fill_between(x, y2, alpha = 0.3, color = "cyan")
ax.set_title(title)
ax.legend()
fig, axes = plt.subplots(2, n_biomarkers//2, figsize=(20, 10))
for i, biomarker in enumerate(biomarkers):
ax = axes.flatten()[i]
mu1, sigma1, mu2, sigma2 = real_theta_phi[
real_theta_phi.biomarker == biomarker].reset_index().iloc[0, :][2:].values
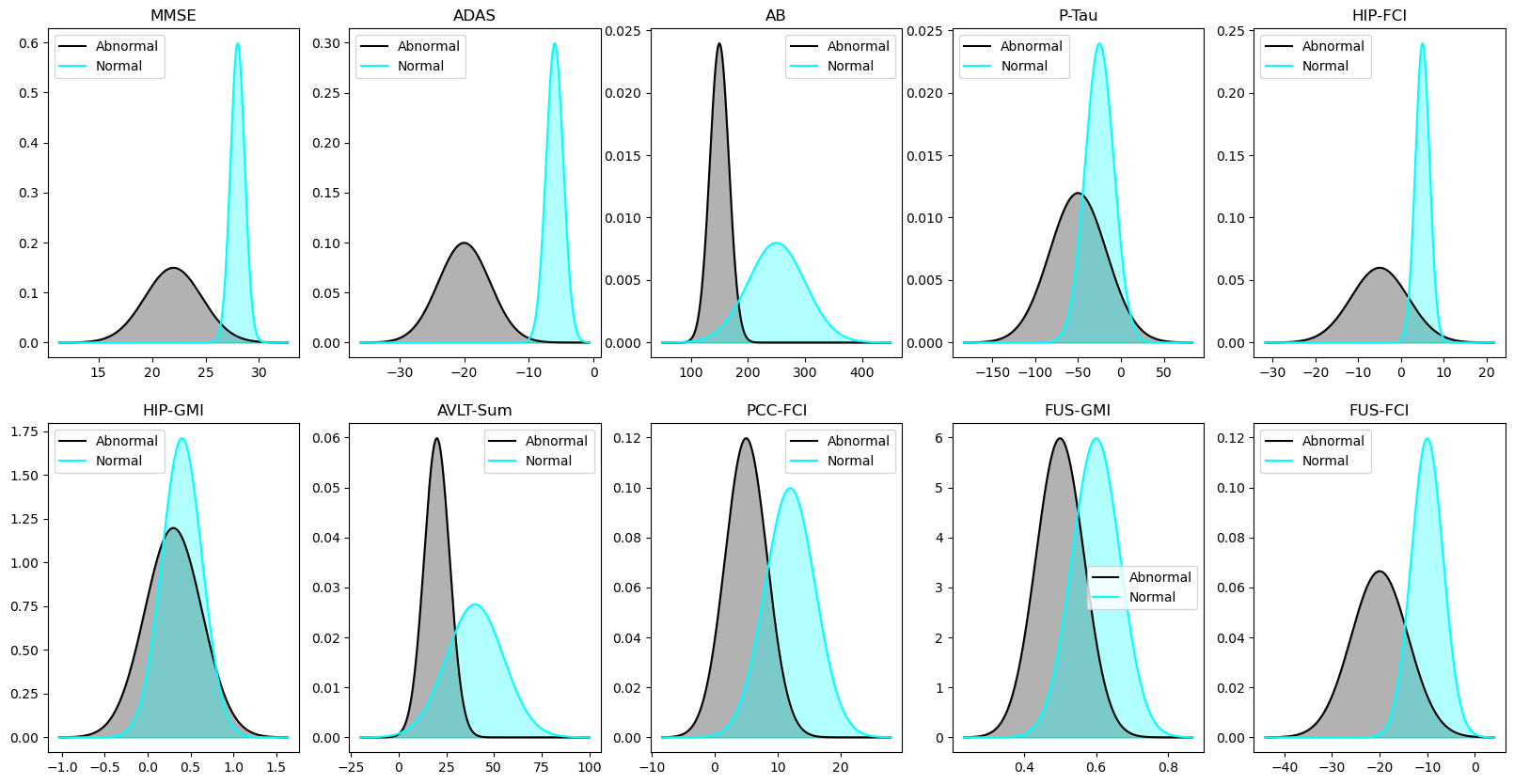
plot_distribution_pair(
ax, mu1, sigma1, mu2, sigma2, title = biomarker)You can compare this to Figure 3.1.
3.2 The Generating Process
In the following, we explain our data generation process.
We have the following parameters:
\(J\): Number of participants.
\(R\): The percentage of healthy participants.
\(M\): Number of datasets per combination of \(j\) and \(r\).
We set these parameters:
js = [50, 200, 500]
rs = [0.1, 0.25, 0.5, 0.75, 0.9]
num_of_datasets_per_combination = 50So, there will be \(3 \times 5 \times 50 = 750\) datasets to be generated.
We define our generate_data_from_ebm function:
Code
def generate_data_from_ebm(
n_participants: int,
S_ordering: List[str],
real_theta_phi_file: str,
healthy_ratio: float,
output_dir: str,
m, # combstr_m
seed: Optional[int] = 0
) -> pd.DataFrame:
"""
Simulate an Event-Based Model (EBM) for disease progression.
Args:
n_participants (int): Number of participants.
S_ordering (List[str]): Biomarker names ordered according to the order
in which each of them get affected by the disease.
real_theta_phi_file (str): Directory of a JSON file which contains
theta and phi values for all biomarkers.
See real_theta_phi.json for example format.
output_dir (str): Directory where output files will be saved.
healthy_ratio (float): Proportion of healthy participants out of n_participants.
seed (Optional[int]): Seed for the random number generator for reproducibility.
Returns:
pd.DataFrame: A DataFrame with columns 'participant', "biomarker", 'measurement',
'diseased'.
"""
# Parameter validation
assert n_participants > 0, "Number of participants must be greater than 0."
assert 0 <= healthy_ratio <= 1, "Healthy ratio must be between 0 and 1."
# Set the seed for numpy's random number generator
rng = np.random.default_rng(seed)
# Load theta and phi values from the JSON file
try:
with open(real_theta_phi_file) as f:
real_theta_phi = json.load(f)
except FileNotFoundError:
raise FileNotFoundError(f"File {real_theta_phi} not fount")
except json.JSONDecodeError:
raise ValueError(
f"File {real_theta_phi_file} is not a valid JSON file.")
n_biomarkers = len(S_ordering)
n_stages = n_biomarkers + 1
n_healthy = int(n_participants * healthy_ratio)
n_diseased = int(n_participants - n_healthy)
# Generate disease stages
kjs = np.concatenate((np.zeros(n_healthy, dtype=int),
rng.integers(1, n_stages, n_diseased)))
# shuffle so that it's not 0s first and then disease stages bur all random
rng.shuffle(kjs)
# Initiate biomarker measurement matrix (J participants x N biomarkers) with None
X = np.full((n_participants, n_biomarkers), None, dtype=object)
# Create distributions for each biomarker
theta_dist = {biomarker: stats.norm(
real_theta_phi[biomarker]['theta_mean'],
real_theta_phi[biomarker]['theta_std']
) for biomarker in S_ordering}
phi_dist = {biomarker: stats.norm(
real_theta_phi[biomarker]['phi_mean'],
real_theta_phi[biomarker]['phi_std']
) for biomarker in S_ordering}
# Populate the matrix with biomarker measurements
for j in range(n_participants):
for n, biomarker in enumerate(S_ordering):
# because for each j, we generate X[j, n] in the order of S_ordering,
# the final dataset will have this ordering as well.
k_j = kjs[j]
S_n = n + 1
# Assign biomarker values based on the participant's disease stage
# affected, or not_affected, is regarding the biomarker, not the participant
if k_j >= 1:
if k_j >= S_n:
# rvs() is affected by np.random()
X[j, n] = (
j, biomarker, theta_dist[biomarker].rvs(random_state=rng), k_j, S_n, 'affected')
else:
X[j, n] = (j, biomarker, phi_dist[biomarker].rvs(random_state=rng),
k_j, S_n, 'not_affected')
# if the participant is healthy
else:
X[j, n] = (j, biomarker, phi_dist[biomarker].rvs(random_state=rng),
k_j, S_n, 'not_affected')
df = pd.DataFrame(X, columns=S_ordering)
# make this dataframe wide to long
df_long = df.melt(var_name="Biomarker", value_name="Value")
data = df_long['Value'].apply(pd.Series)
data.columns = ['participant', "biomarker",
'measurement', 'k_j', 'S_n', 'affected_or_not']
# biomarker_name_change_dic = dict(
# zip(S_ordering, range(1, n_biomarkers + 1)))
data['diseased'] = data.apply(lambda row: row.k_j > 0, axis=1)
# data.drop(['k_j', 'S_n', 'affected_or_not'], axis=1, inplace=True)
# data['biomarker'] = data.apply(
# lambda row: f"{row.biomarker} ({biomarker_name_change_dic[row.biomarker]})", axis=1)
if not os.path.exists(output_dir):
os.makedirs(output_dir)
filename = f"{int(healthy_ratio*n_participants)}|{n_participants}_{m}"
data.to_csv(f'{output_dir}/{filename}.csv', index=False)
# print("Data generation done! Output saved to:", filename)
return dataS_ordering = np.array([
'HIP-FCI', 'PCC-FCI', 'AB', 'P-Tau', 'MMSE', 'ADAS',
'HIP-GMI', 'AVLT-Sum', 'FUS-GMI', 'FUS-FCI'
])
# where the generated data will be saved
output_dir = 'data'
# We run the following only once; once the data is generated, we no longer run it
# We still show the codes to present our generation process
torun = Falseif torun:
real_theta_phi_file = 'files/real_theta_phi.json'
for j in js:
for r in rs:
for m in range(0, num_of_datasets_per_combination):
generate_data_from_ebm(
n_participants=j,
S_ordering=S_ordering,
real_theta_phi_file=real_theta_phi_file,
healthy_ratio=r,
output_dir=output_dir,
m=m,
seed = int(j*10 + (r * 100) + m),
)
print(f'Done for J={j}')3.3 Visualize Synthetic Data
Above, we have generated 750 datasets, named in the fashion of 150|200_3, which means the third dataset when \(j = 200\) and \(r = 0.75\).
Next, we try to visualize this dataset.
df = pd.read_csv(f"{output_dir}/150|200_3.csv")
df.head()| participant | biomarker | measurement | k_j | S_n | affected_or_not | diseased | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | HIP-FCI | 3.135981 | 0 | 1 | not_affected | False |
| 1 | 1 | HIP-FCI | 12.593704 | 2 | 1 | affected | True |
| 2 | 2 | HIP-FCI | 6.220776 | 0 | 1 | not_affected | False |
| 3 | 3 | HIP-FCI | 3.545100 | 0 | 1 | not_affected | False |
| 4 | 4 | HIP-FCI | 3.966541 | 0 | 1 | not_affected | False |
df.shape(2000, 7)This dataset has \(2000\) rows because we have \(200\) participants and \(10\) biomarkers.
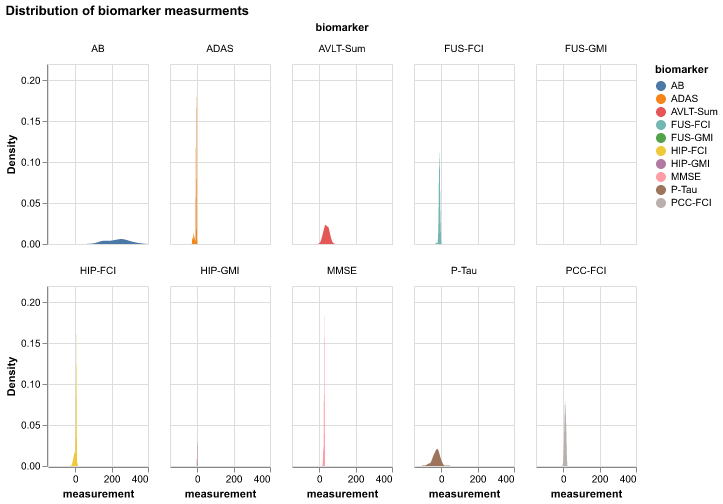
3.3.1 Distribution of all biomarker values
Code
alt.renderers.enable('png')
alt.Chart(df).transform_density(
'measurement',
as_=['measurement', 'Density'],
groupby=['biomarker']
).mark_area().encode(
x="measurement:Q",
y="Density:Q",
facet = alt.Facet(
"biomarker:N",
columns = 5
),
color=alt.Color(
'biomarker:N'
)
).properties(
width= 100,
height = 180,
).properties(
title='Distribution of biomarker measurments'
)3.3.2 Distribution of A Specific Biomarker
Code
idx = 1
biomarkers = df.biomarker.unique()
bio_data = df[df.biomarker==biomarkers[idx]]
alt.Chart(bio_data).transform_density(
'measurement',
as_=['measurement', 'Density'],
groupby=['affected_or_not']
).mark_area().encode(
x="measurement:Q",
y="Density:Q",
facet = alt.Facet(
"affected_or_not:N",
),
color=alt.Color(
'affected_or_not:N'
)
).properties(
width= 240,
height = 200,
).properties(
title=f'Distribution of {biomarker} measurements'
)3.3.3 Looking into A Specific Participant
pidx = 1
p_data = df[df.participant == pidx]
p_data| participant | biomarker | measurement | k_j | S_n | affected_or_not | diseased | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | HIP-FCI | 12.593704 | 2 | 1 | affected | True |
| 201 | 1 | PCC-FCI | 7.164017 | 2 | 2 | affected | True |
| 401 | 1 | AB | 182.033823 | 2 | 3 | not_affected | True |
| 601 | 1 | P-Tau | -25.345325 | 2 | 4 | not_affected | True |
| 801 | 1 | MMSE | 27.600823 | 2 | 5 | not_affected | True |
| 1001 | 1 | ADAS | -4.920415 | 2 | 6 | not_affected | True |
| 1201 | 1 | HIP-GMI | 0.099052 | 2 | 7 | not_affected | True |
| 1401 | 1 | AVLT-Sum | 30.270797 | 2 | 8 | not_affected | True |
| 1601 | 1 | FUS-GMI | 0.658954 | 2 | 9 | not_affected | True |
| 1801 | 1 | FUS-FCI | -11.701559 | 2 | 10 | not_affected | True |
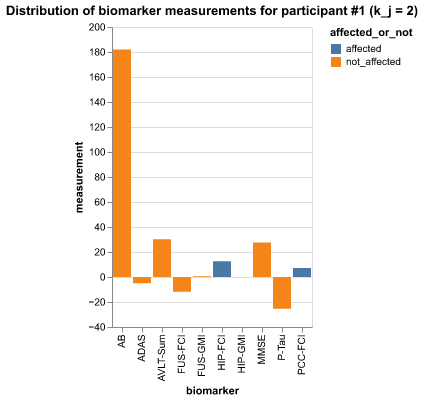
Code
pidx =1 # participant index
p_data = df[df.participant == pidx]
alt.Chart(p_data).mark_bar().encode(
x='biomarker',
y='measurement',
color=alt.Color(
'affected_or_not:N'
),
tooltip=['biomarker', 'affected_or_not', 'measurement']
).interactive().properties(
title=f'Distribution of biomarker measurements for participant #{idx} (k_j = {p_data.k_j.to_list()[0]})'
)