2 EBM Explained

2.1 Overview of Event-Based Model (EBM)

EBM provides a statistical model to understand disease progression through biomarkers. Using EBM, we can estimate the likelihood of biomarker measurements or generate synthetic data of biomarker measurements.

EBM can be used in two main ways:

Calculate the likelihood of biomarker measurements
Generate biomarker measurements

2.2 Key Concepts

Suppose the order in which a disease affects biomarkers is \(S\). For example, \(S\) = [‘biomarker1’, ‘biomarker3’, ‘biomarker2’].

We also suppose biomarker measurements follow Gaussian distributions. When a biomarker is affected by the disease, its distribution parameters (mean and standard deviation) are denoted by \(\theta\). If not affected, \(\phi\).

The disease stage of a participant is \(k_j\). To simplify things, let us assume the total number of disease stages is equal to the number of biomarkers.

2.3 Calculate the Likelihood of Biomarker Measurements

Suppose we have one participant’s measurement data of five biomarkers:

Now, the question is:

What is the likelihood of this participant having this sequence of biomarker data, given that we know \(S, \theta, \phi\).

As defined above, \(S\) is the order in which different biomarkers get affected by the disease. It is the column of \(S_n\) in the above data.

\(\theta\) for each biomarker is the \(\mu\) and \(\alpha\) of normal distribution of biomarker measurement when the biomarker is affected by the disease.

\(\phi\) for each biomarker is the \(\mu\) and \(\alpha\) of normal distribution of biomarker measurement when the biomarker is NOT affected by the disease.

The column of participant is simply this participant’s identification in the data.

The column of affected_or_not refers to whether a biomarker is affected by the disease. It is affected if \(k_j \ge S_n\); otherwise, not affected. This column is not available if we do not have access to the column of \(k_j\), which stands for this participant’s disease stage.

The column of Diseased refers to whether this participant is healthy (i.e., \(k_j = 0\)) or diseased (i.e., \(k_j \ge 1\)).

In the following, we explain how to calculate this likelihood in two scenarios: (1) known \(k_j\) and (2) unknown \(k_j\).

2.3.1 Known \(k_j\)

\[ p(X_{j} | S, z_j = 1, k_j) = \underbrace{\prod_{i=1}^{k_j}{p(X_{S(i)j} \mid \theta_{S(i)} )}}_{\text{Affected biomarker likelihood}} \, \underbrace{\prod_{i=k_j+1}^N{p(X_{S(i)j} \mid \phi_{S(i)})}}_{\text{Non-affected biomarker likelihood}} \tag{2.1}\]

This equation computes the likelihood of the observed biomarker data of a specific participant, given that we know the disease stage this patient is at (\(k_j\)).

\(S\) is an ordered array of biomarkers that are affected by the disease, for example, \([b, a, d, c]\). This means that biomarker \(b\) is affected at stage 1. At stage 2, biomarker \(b\) and \(a\) will be affected.
\(S(i)\) is the \(i^{th}\) biomarker according to \(S\). For example \(S_1\) will be biomarker \(b\).
\(k_j\) indicates the stage the patient is at, for example, \(k_j = 2\). This means that the disease has affected biomarkers \(a\) and \(b\). Biomarker \(c\) and \(d\) have not been affected yet.
\(\theta_{S(i)}\) is the parameters for the probability density function (PDF) of observed value of biomarker \(S(i)\) when this biomarker has been affected by the disease. Let’s assume this distribution is a Gaussian distribution with means of \([45, 50, 55, 60]\) and a standard deviation of \(5\) for biomarker \(b\), \(a\), \(d\), and \(c\).
\(\phi_{S(i)}\) is the parameters for the probability density function (PDF) of observed value of biomarker \(S(i)\) when this biomarker has NOT been affected by the disease. Let’s assume this distribution is a Gaussian distribution with means of \([25, 30, 35, 40]\) and a standard deviation of \(3\) for biomarker \(b\), \(a\), \(d\), and \(c\).
\(X_j\) is an array representing the patient’s observed data for all biomarkers. Assume the data is \([77, 45, 53, 90]\) for biomarkers \(b\), \(a\), \(d\), and \(c\).

We assume that the patient is at stage \(2\) of this disease; hence \(k_j = 2\).

Next, we are going to calculate \(p(X_j|S, z_j = 1, k_j)\):

When \(i = 1\), we have \(S_{(i)} = b\) and \(X_{S_{(i)}} = X_b = 45\). So

\[p(X_{S_{(i)}} | \theta_{S(i)}) = \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{X_b - \mu}{\sigma} \right)^2}\]

Because \(k_j = 2\), so biomarker \(b\) and \(a\) are affected. We should use the distribution of \(\theta_b\); therefore, we should plug in \(\mu = 45, \sigma = 5\) in the above equation.

We can do the same for \(i\) = 2, 3, and 4.

The above is the likelihood of the given biomarker data when \(k_j = 2\).

Note that \(p (X_b | \theta_b)\) is probability density, a value of a probability density function at a specific point; so it is not a probability itself.

Multiplying multiple probability densities will give us a likelihood.

2.3.2 Unknown \(k_j\)

\[ P(X_{j} | S) = \sum_{k_j=0}^N{P(k_j) p(X_{j} \mid S, k_j)} \tag{2.2}\]

Suppose we have the same information above, except that we do not know at which disease stage the patient is, i.e., we do not know \(k_j\). We have the observed biomarker data: \(X_j = [77, 45, 53, 90]\). And I wonder: what is the likelihood of seeing this specific observed data?

We assume that all five stages (including \(k_j = 0\)) are equally likely.

We do not know \(k_j\), so the best option is to calculate the “average” likelihood of all the biomarker data.

Based on Equation 2.1, we can calculate the following:

\(L_1 = p(X_j | S, k_j = 1)\)

\(L_2 = p(X_j | S, k_j = 2)\)

\(L_3 = p(X_j | S, k_j = 3)\)

\(L_4 = p(X_j | S, k_j = 4)\)

If this participant is healthy, then we know \(k_j = 0\), therefore:

If this participant is diseased but we do not know the actual \(k_j\), we can estimate it this way

\(P(k_j)\) is the prior likelihood of being at stage \(k\). Event based models assume a uniform prior on \(k_j\). Therefore:

\(P(X_{j} | z_j=1, S) = \frac{1}{4} \left(L_1 + L_2 + L_3 + L_4 \right)\)

Tip

When this participant is diseased but we do not know the actual stage of this participant, the above method is useful also because it hints at the relative likelihood of each possible stage. For example, if L2 is much larger than L1, L3, and L4, then we know this participant is most likely to be at stage 2.

2.3.3 Extension

If we are more interested in the likelihood of a whole dataset consisting of all participants, we multiply all participants’ likelihood: \(L = L_{P_1} \times L_{P_2} \times L_{P_3} ... \times L_{P_j}\). Because this number tends to be very large, we take the natural log of \(L\), i.e., \(\ln(L)\).

2.4 EBM as A Generative Model

We can use EBM to generate synthetic biomarker data if we know:

The order (\(S\)) in which different biomarkers get affected by the disease.
Parameters (i.e., mean and standard deviation) of biomarkers’ distribution when they are affected (\(\theta\)) and not affected (\(\phi\)) by the disease.
Stages (\(k_j\)) that each participant is in.

Data we can generate looks like Figure 2.1.

This data is from a single participant.

As we mentioned above, to generate this data, we need to know:

\(S\), i.e., the order of biomarkers. In the above example, \(S\) is HIP-FCI, PCC-FCI, HIP-GMI, FUS-GMI, FUS-FCI.
\(\mathcal N(\theta_{\mu}, \theta_{\sigma})\) and \(\mathcal N(\phi_{\mu}, \phi_{\sigma})\) for each of the five biomarkers, which are known but not shown directly here in the dataset.
\(k_j\), which is 2 in the above example.

We explain how this data is constructed in the following, column by column.

First, the participant id is \(67\). The biomarker indicates each of the five biomarkers examined and measured. The measurement is the biomarkers’ measurement. k_j is the participant’s stage. If this stage is above 0, it means Diseased = True. S_n indicates the \(n\)-th rank in the order. If k_j < S_n, it means the participant’s stage hasn’t reached that biomarker’s rank; therefore, this biomarker is not affected. If k_j >= S_n, then this biomarker is affected.

If a biomarker is affected, then its measurement comes from \(\mathcal N(\theta_{\mu}, \theta_{\sigma})\) of that biomarker; if not_affected, \(\mathcal N(\phi_{\mu}, \phi_{\sigma})\).

2.4.1 Generative Process

The generative process of biomarker measurements can be described as:

\[ \begin{split} X_{nj} \mid S, k_j, \theta_n, \phi_n &\sim I(z_j = 1) \bigg[ I(S(n) \leq k_j) \, p(X_{nj} \mid \theta_{n}) \\ &\quad + I(S(n) > k_j) \, p(X_{nj} \mid \phi_{n}) \bigg] \\ &\quad + \left(1 - I(z_j = 1) \right) p(X_{nj} \mid \phi_{n}) \end{split} \tag{2.3}\]

This model says that given that we know \(S, k_j, \theta_n, \text{and } \phi_n\), we can draw the biomarker measurement from a distribution.

\(S \sim \mathrm{UniformPermutation}(\cdot)\)

\(S\) follows a distribution of uniform permutation. That means the ordering of biomarkers is random.

\(k_j \sim \mathrm{DiscreteUniform}(N)\)

\(k_j\) follows a discrete uniform distribution, which means a participant is equally likely to fall in a progression stage (e.g., from \(0\) to \(5\), where \(0\) indicates this participant is healthy.)

2.4.2 Graphical Explanation

In the following, we explain the generative model in three different scenarios using graphical models: (1) All participants are healthy; (2) Both healthy and diseased participants, but all biomarkers are affected among diseased people; (3) Both healthy and diseased participants, but we do not whether biomarkers are affected or not among patients.

2.4.2.1 Scenario 1

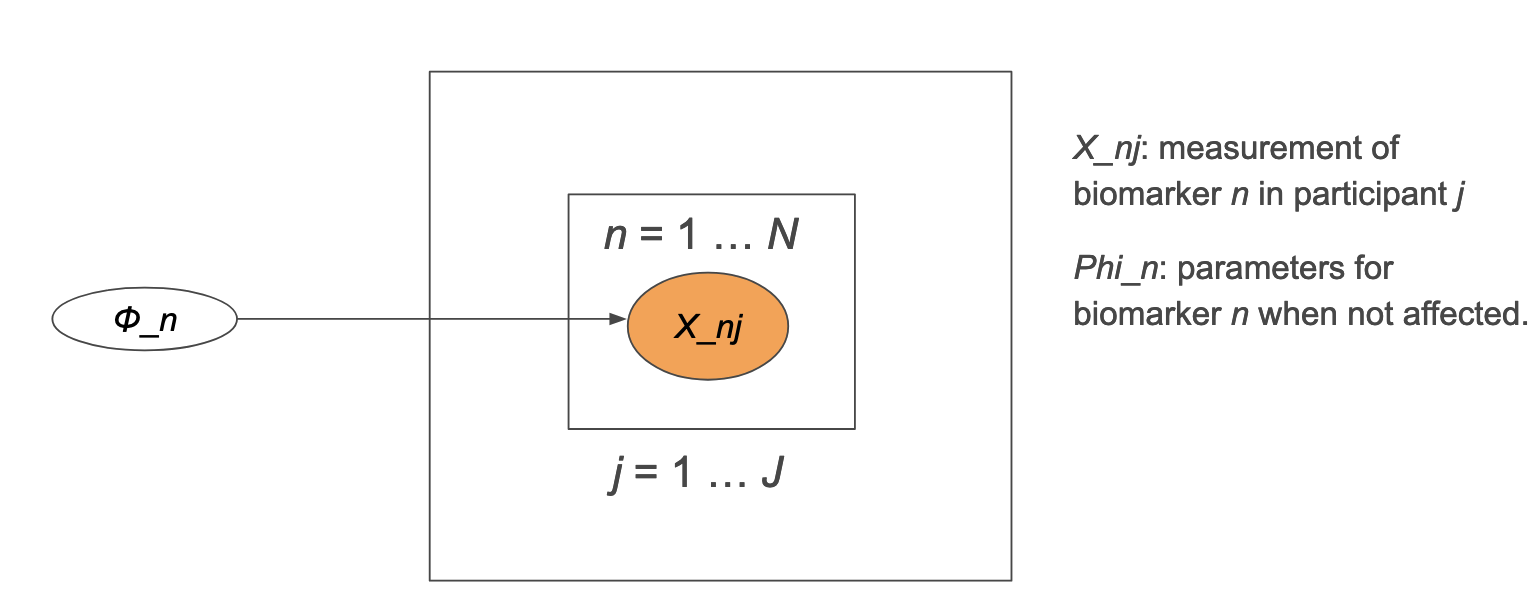
If all participants are healthy:

\[ X_{nj} \sim p(X_{nj} \mid \phi_{n}) \tag{2.4}\]

Where

\(X_{nj}\) indicates the measurement of biomarker \(n\) in participant \(j\).

\(\phi_{n}\) represents \(\mathcal N(\phi_{\mu}, \phi_{\sigma})\) for biomarker \(n\).

The graphical model would look like:

Figure 2.2: Graphical Model of Scenario 1

2.4.2.2 Scenario 2

If we have both diseased and healthy participants, and all biomarkers are affected among deceased participants.

\[ X_{nj} \sim I(z_j == 1) p(X_{nj} \mid \theta_n) + (1-I(z_j == 1))p(X_{nj} \mid \phi_n) \tag{2.5}\]

Where:

\(z_j = 1\) indicates this participant is diseased and \(z_j = 1\) represents a healthy participant.

\(I(True) = 1\) and \(I(False) = 0\).

\(\theta_{n}\) represents \(\mathcal N(\theta_{\mu}, \theta_{\sigma})\) for biomarker \(n\).

The graphical model would look like:

Figure 2.3: Graphical Model of Scenario 2

2.4.2.3 Scenario 3

If we have both healthy and diseased participants, but we do not know whether biomarkers are affected or not among patients, see Equation 2.3.

This is the model in usual cases.

The graphical model looks like:

Figure 2.4: Graphical Model of Scenario 3